WealthC
Perform a linear regression and compute the MSE. Standardize the features and again computer the MSE. Compare the coefficients from each of the two models and describe how they have changed
The 𝑅^2 value of the non-standardized data is 0.7335385259217961and the MSE is 0.4466387646252814. Both coefficients are good indicators that the features can somewhat accurately predict the target variable, wealthC. The 𝑅2 value is fairly close to +1, meaning there is a postive correlation between the features and target and the MSE is fairly close to 0, which means that the difference between the model’s prediction and the actual target values is fairly small. However, if possible we’d like to minimize this difference even more.
Standardizing the data did not change the results. The purpose of standardizing data is to minimize the difference between the scales of features while maintaining the difference in teh range of values. However, because most of our data is binary, the features are already on the same scale. Therefore, standardization is unhelpful in this case.
Run a ridge regression and report your best results.
Optimum alpha value was 1.616 and gave a test data score of 0.7328 and a train data score of 0.734. When I computed the MSE, the minimum test MSE was 0.446 and minium train MSE was 0.433. While these values did not change much from the linear regression, they do indicate that the model is well fit, since the testing and training scores are very close
Run a lasso regression and report your best results.
The optimal alpha value was 0 and gave the test data score of 0.733 and train data score of 0.734. Like the Ridge regression, the Lasso regression did not improve the training or testing score. However, the MSE changed drastically. For Lasso regression the MSE rose to 1.67 for both the training and testing data. Becuase the MSE was so much worse, I believe Lasso is not the best model.
WealthI
Perform a linear regression and compute the MSE. Standardize the features and again computer the MSE. Compare the coefficients from each of the two models and describe how they have changed Similar to the wealthC, standardizing the data did not do much to increase the 𝑅^2 value. For wealthI, the coefficient of determination was 0.824, which is marginally better than the results of wealthC. However, the MSE was gregariously large, which is concerning. The MSE for both the standardized and non-standardized data was 1,773,535,271, which should mean that the model is able to accurately predict the target variable.
Run a ridge regression and report your best results.
The optimal alpha value for the Ridge model was 1.010 and yielded a testing and training data score of 0.823 and 0.824 respectively. This did not improve from the linear regression model. Furthermore, the MSE of both the testing and training data still hovered around 1,770,000,000 for both the testing and training data.
Run a lasso regression and report your best results.
The optimal value for the Lasso regression was 0.00 and had the same $R^2$ and MSE values as the linear and ridge model.
Which of the models produced the best results in predicting wealth of all persons throughout the smaller West African country being described? Support your results with plots, graphs and descriptions of your code and its implementation. You are welcome to incorporate snippets to illustrate an important step, but please do not paste verbose amounts of code within your project report. Alternatively, you are welcome to provide a link in your references at the end of your (part 1) Project 5 report.
The model that produced the best results in predicting wealth of all persons throughout the smaller West African country was the linear regression model of the target wealthI. This model was the best becuase it had the highest 𝑅^2 value as well as the lowest MSE. Both these values indicate that the data is fairly correlated and the feautures can be used to predict the target value fairly well.
In deciding the best model I went through and modeled the data’s ability to predict both wealthC and wealthI using linear, ridge, and lasso regression. For the first run-through of linear regression I attempted to standardize the data to see if it would increase the $R^2$, but standardizing had little affect. From then on I only used the original data in modeling. When calculating linear regression I also plotted the predicted vs observed data to see if I could observe any general trends:
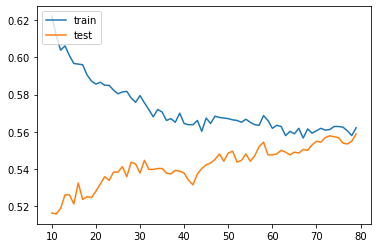
Not only does this graph confirm the upward trend that the $R^2$ value already indicated, it shows that the predicted and the observed were close together. Both the y and x axis are bewteen 1 and 6 and while it would be ideal that the values are clustered closer together, what we are observing is pretty good. To take a closer look at this, I calculated the MSE and plotted the difference between the predicted and observed values:
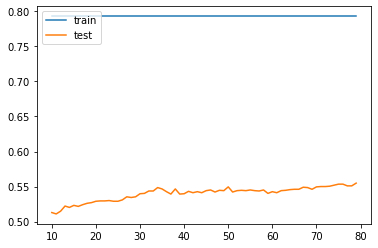
As you can see in the graph above, the MSE for the linear regression model of wealthI centered around 0, which is what we want from a predictive model. As stated before, the MSE for the model was 0.447.
After my initial observations, I continued testing different models, getting both the MSE and the $R^2$ values, but no other model performed as well as the linear regression model of WealthI.